高等数学

5 定积分1

6 微分方程2

7 立体几何3

8 多元函数微分法及其应用4

10 级数5

Also view at 纯文本

  1. 5 定积分

    5.pdf

    1. <<assets/5-20250627103546-grij4xb.pdf/20250627103847-4yhxquz "曲边梯形">>

    2. <<assets/5-20250627103546-grij4xb.pdf/20250627103804-f4lrdx2 "定积分的定义">>

      1. <<assets/5-20250627103546-grij4xb.pdf/20250627103957-7w8bty5 "定积分的结果是数，可正可负，求导后 一定是 0 ">>

      2. <<assets/5-20250627103546-grij4xb.pdf/20250627104033-kwnvx7t "可积的充分条件定理">>

      3. <<assets/5-20250627103546-grij4xb.pdf/20250627104124-51zqwmx "定积分的性质">>

        image

    3. <<assets/5-20250627103546-grij4xb.pdf/20250627174526-tfxc44n "牛顿-莱布尼斯 在积分上限函数中">>

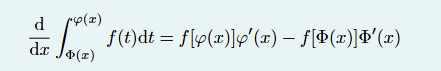
      image

      注意，被积函数与变量 x 无关. 如果有关则为拓展式

      \frac{\d}{\d x}\int_{\Phi(x)}^{\varphi(x)}f(t,x)\ \d t = f[\varphi(x),x]\varphi'(x) - f(\Phi(x),x)\Phi'(x) + \int_{\Phi(x)}^{\varphi(x)}\frac{\partial}{\partial x}f(t,x)\ \mathrm{d}t

    4. <<assets/5-20250627103546-grij4xb.pdf/20250627180355-xr1wdv5 "换元必换限">>

    5. <<assets/5-20250627103546-grij4xb.pdf/20250627181235-wa98r7w "偶倍奇零">>

    6. <<assets/5-20250627103546-grij4xb.pdf/20250627181700-r98gjgh "sin和cos的积分">>

      \begin{aligned}I_n&=\int_0^{\frac{\pi}{2}}\sin^nx\mathrm{d}x\\&=\int_0^{\frac{\pi}{2}}\cos^nx\mathrm{d}x\\&=\begin{cases}\frac{n-1}{n}\cdot\frac{n-3}{n-2}\cdots\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2},&n\text{为正偶数}\\\frac{n-1}{n}\cdot\frac{n-3}{n-2}\cdots\frac{4}{5}\cdot\frac{2}{3},&n\text{为大于1的奇数}&\end{cases}\end{aligned}

    7. <<assets/5-20250627103546-grij4xb.pdf/20250627214836-4wj3fau "极坐标下的面积元素">>

    8. <<assets/5-20250627103546-grij4xb.pdf/20250627214919-x2cmcxf "旋转体">>

    9. <<assets/5-20250627103546-grij4xb.pdf/20250627214610-rfob1xp "平面曲线的弧长">>

      \text{曲线方程}\begin{cases}\text{直角坐标方程}&ds=\sqrt{1+{y^{\prime}}^{2}}\mathrm{d}x\\\text{参数方程方程}&ds=\sqrt{{\varphi^{\prime}}^{2}(t)+{\psi^{\prime}}^{2}(t)}\mathrm{d}t\\\text{极坐标方程}&ds=\sqrt{\rho^{2}(\varphi)+{\rho^{\prime}}^{2}(\varphi)}\mathrm{d}\varphi&\end{cases}

    ‍ ↩

  2. 6 微分方程

    6.pdf

    1. <<assets/6-20250627215017-e9dn4fg.pdf/20250627215049-24lgc1t "微分方程的基本概念">>

    2. <<assets/6-20250627215017-e9dn4fg.pdf/20250627215633-t73ktfp "可分离变量的微分方程">>

      f(x)\mathrm{d}x=g(y)\mathrm{d}y

    3. <<assets/6-20250627215017-e9dn4fg.pdf/20250627215853-k69rksa "一阶齐次线性微分方程的通解">>

      y=Ce^{-\int P(x)\mathrm{d}x}

    4. <<assets/6-20250627215017-e9dn4fg.pdf/20250627220143-y3ha87b "一阶非齐次线性微分方程">>

      {y=\left[\int Q(x)e^{\int P(x)\mathrm{d}x}\mathrm{d}x+C\right]e^{-\int P(x)\mathrm{d}x}}

    5. <<assets/6-20250627215017-e9dn4fg.pdf/20250627221216-i34f4gh "二阶非齐次线性方程通解">>

    ‍ ↩

  3. 7 立体几何

    7.pdf

    1. <<assets/7-20250627221616-8db0l9f.pdf/20250627221706-b4nbqwm "定比分点">>
    2. <<assets/7-20250627221616-8db0l9f.pdf/20250627221832-f8kgvvn "向量的方向角与方向余弦">>
    3. ‍

    ‍ ↩

  4. 8 多元函数微分法及其应用

    8.1.pdf

    ‍ ↩

  5. 10 级数

    1 级数的定义

    • 无穷级数

      \sum_{n=1}^{\infty}a_n:=\lim_{N\to\infty}\sum_{n=1}^{N}a_n =\lim_{N\to\infty}S_N,\qquad S_N\text{称为第 }N\text{ 部分和}

      极限存在 ⇒ 级数 收敛，极限值记作 ​S；否则 发散。

    • 绝对收敛与条件收敛
      若 ​\sum|a_n| 收敛 ⇒ ​\sum a_n 绝对收敛（必收敛）；
      若 ​\sum a_n 收敛而 ​\sum|a_n| 发散 ⇒ 条件收敛。

    2 级数的性质

    性质 说明
    线性 若​\sum a_n,\sum b_n 收敛，则 ​\sum(\alpha a_n+\beta b_n) 收敛且和为 ​\alpha\sum a_n+\beta\sum b_n。
    正项单调有界 若​a_n\ge0，则部分和单调不降；是否收敛仅取决于是否有界。

    3 级数审敛法

    3.1 正项级数审敛法（​a_n\ge0）

    比较判别法

    与已知收敛/发散的正项级数比较

    • 若 ​a_n\leq b_n 且 ​b_n 收敛，则 ​a_n 收敛。
    • 若 ​a_n\geq b_n 且 ​b_n 发散，则 ​b_n 发散。

    口诀：大收则小收，小发则大发。

    极限审敛法

    若 ​a_n 和 ​b_n 均为正项级数，设 ​L = \frac{a_n}{b_n} 则

    • ​L \in(0,+\infty)\Rightarrow 同敛散
    • ​L = 0 \Rightarrow 同敛（若收敛则相同）
    • ​L = \infty \Rightarrow 同散（若发散则相同）

    比值判别法

    设

    n+1}}{a_n}

    则

    • ​\rho<1，收敛
    • ​\rho>1，发散
    • ​\rho>1，判断失败

    3.2 交错级数审敛法

    • Leibniz 判别法（经典交错级数）：

      \left| a_n \right|单调递减，且\lim_{n \to \infty}\left| a_n \right|= 0,\quad\Longrightarrow\quad \sum_{n=1}^{\infty}(-1)^{n-1}a_n \text{ 收敛}

    • 绝对/条件收敛判别
      先用绝对值判别；若失败，再尝试 Leibniz 判别法1

    3.3 任意项级数审敛法

    通过绝对收敛转为正项级数1

    ‍

    4 常见级数及其证明

    4.1 列表

    级数 收敛性结论
    #调和级数#​\displaystyle\sum_{n=1}^{\infty}\frac1n 发散
    #几何级数#​\displaystyle\sum_{n=0}^{\infty}p^{\,n} ​| p | <1 收敛； ​| p | \ge 1 发散
    #p-级数#​\displaystyle\sum_{n=1}^{\infty}\frac1{n^{p}} ​p>1 收敛；​p\le1 发散

    下文逐一给出简洁证明。

    4.2 #调和级数# ​\sum\limits_{n=1}^{\infty}\frac1n 发散

    • 积分判别法：

      \int_{1}^{N}\frac{1}{x}\,dx=\ln N\to\infty\quad\Longrightarrow\quad\sum_{n=1}^{\infty}\frac1n \text{ 发散}

    • Cauchy 折半法：

      \sum_{n=2^{k-1}+1}^{2^{k}}\frac1n \;>\;\frac{2^{k-1}}{2^{k}}=\tfrac12

      每组和 ≥ ½，累加无界 ⇒ 发散。

    4.3 #几何级数# ​\sum_{n=0}^{\infty}p^{\,n}

    • 若 ​|p|<1：
      部分和 ​S_N=\dfrac{1-p^{N+1}}{1-p}\xrightarrow{N\to\infty}\dfrac1{1-p} ⇒ 收敛，和为 ​(1-p)^{-1}。
    • 若 ​|p|\ge1：
      ​|p^{\,n}|\not\to0 或项不减 ⇒ 必发散。

    4.4 #p-级数# ​\sum_{n=1}^{\infty}\tfrac1{n^{p}}

    • 积分判别法：

      \int_{1}^{\infty}\frac{dx}{x^{p}}= \begin{cases} \dfrac{1}{p-1}, & p>1,\\[6pt] \infty, & p\le1. \end{cases}

      ⇒ ​p>1 收敛；​p\le1 发散。

    • 对 ​p=1 特例：即调和级数，已知发散。 ↩

    • Leibniz 判别法（经典交错级数）：

      ��调递减，且\lim_{n \to \infty}\left| a_n \right|= 0,\quad\Longrightarrow\quad \sum_{n=1}^{\infty}(-1)^{n-1}a_n \text{ 收敛}
      ↩

  7. 3.1 正项级数审敛法（​a_n\ge0）

    比较判别法

    与已知收敛/发散的正项级数比较

    • 若 ​a_n\leq b_n 且 ​b_n 收敛，则 ​a_n 收敛。
    • 若 ​a_n\geq b_n 且 ​b_n 发散，则 ​b_n 发散。

    口诀：大收则小收，小发则大发。

    极限审敛法

    若 ​a_n 和 ​b_n 均为正项级数，设 ​L = \frac{a_n}{b_n} 则

    • ​L \in(0,+\infty)\Rightarrow 同敛散
    • ​L = 0 \Rightarrow 同敛（若收敛则相同）
    • ​L = \infty \Rightarrow 同散（若发散则相同）

    比值判别法

    设

    n+1}}{a_n}

    则

    • ​\rho<1，收敛
    • ​\rho>1，发散
    • ​\rho>1，判断失败 ↩